CAT simulation
Aiden Loe
07 January, 2021
Welcome
This page will give you a general idea of how to simulate a CAT using the catR package.
The developers has made it really easy for us to run simulations.
I am still building the content for this page. So please bear with it.
However, with the limited information you can still run the code and try it yourself.
Load catR package
require(catR)Run CAT simulation
We will be using a polytomous dataset to run our simulation. There are several models that we can use - Graded Response Model (GRM), Modified Graded Response Model (MGRM), Partial Credit Model (PCM), Generalised Partial Credit Model (GPCM), Rating Scale Model (RSM), and Nominal Response Model (NRM). The ones that are more widely used are the GRM, GPCM, PCM. In our example will be using the PCM model.
### Load 'polyIQ' item bank
bank <- read.table("https://www.dropbox.com/s/ml920oyi1z2npid/polyIQ.txt?raw=1",header = TRUE)
bank <- as.matrix(bank)
head(bank)## lambdaj delta1 delta2 delta3
## [1,] -1.732 -1.4 0.3 1.8
## [2,] -1.020 -1.4 0.3 1.8
## [3,] -2.100 -1.4 0.3 1.8
## [4,] -2.535 -1.4 0.3 1.8
## [5,] -1.258 -1.4 0.3 1.8
## [6,] -1.172 -1.4 0.3 1.8### CAT design:
#creation of logic for polytomous is exactly the same for dichtomous items.
## two starting items
startList <- list(nrItems = 2, theta=0)
## next item selection by 'MFI', EAP ad-interim proficiency estimation
testList <- list(method = "EAP", itemSelect = "MFI")
## stop after 10 items
stopList <- list(rule = "length", thr = 10)
## final proficiency estimation using maximum likelihood
finalList <- list(method = "BM")
### generation of a CAT response pattern
res <- randomCAT(trueTheta = 0, itemBank = bank, model="PCM",
start = startList, test = testList, stop = stopList, final = finalList)
## display of the output
res## Random generation of a CAT response pattern
## without fixing the random seed
##
## Item bank calibrated under Partial Credit Model
##
## True ability level: 0
##
## No pre-specified minimum CAT length
##
## Starting parameters:
## Number of early items: 1
## Early item selection: maximum informative items for starting abilities
## Early items not chosen to control for content balancing
## Starting ability: 0
##
## Adaptive test parameters:
## Next item selection method: maximum Fisher information
## Provisional ability estimator: Expected a posteriori (EAP) estimator
## Provisional prior ability distribution: N(0,1) prior
## Ability estimation adjustment for constant pattern: none
## Type of standard error: asymptotic SE (ASE)
## Type of ASE formula: classic formula
##
## Stopping rule:
## Stopping criterion: length of test
## Maximum test length: 10
##
## Randomesque method:
## Number of 'randomesque' starting items: 1
## Number of 'randomesque' test items: 1
##
## Content balancing control:
## No control for content balancing
##
## Adaptive test details:
##
## Nr 1 2 3 4 5 6 7 8 9 10
## Item 21 7 23 22 13 19 20 17 18 12
## Resp. 0 2 2 0 1 2 0 2 2 3
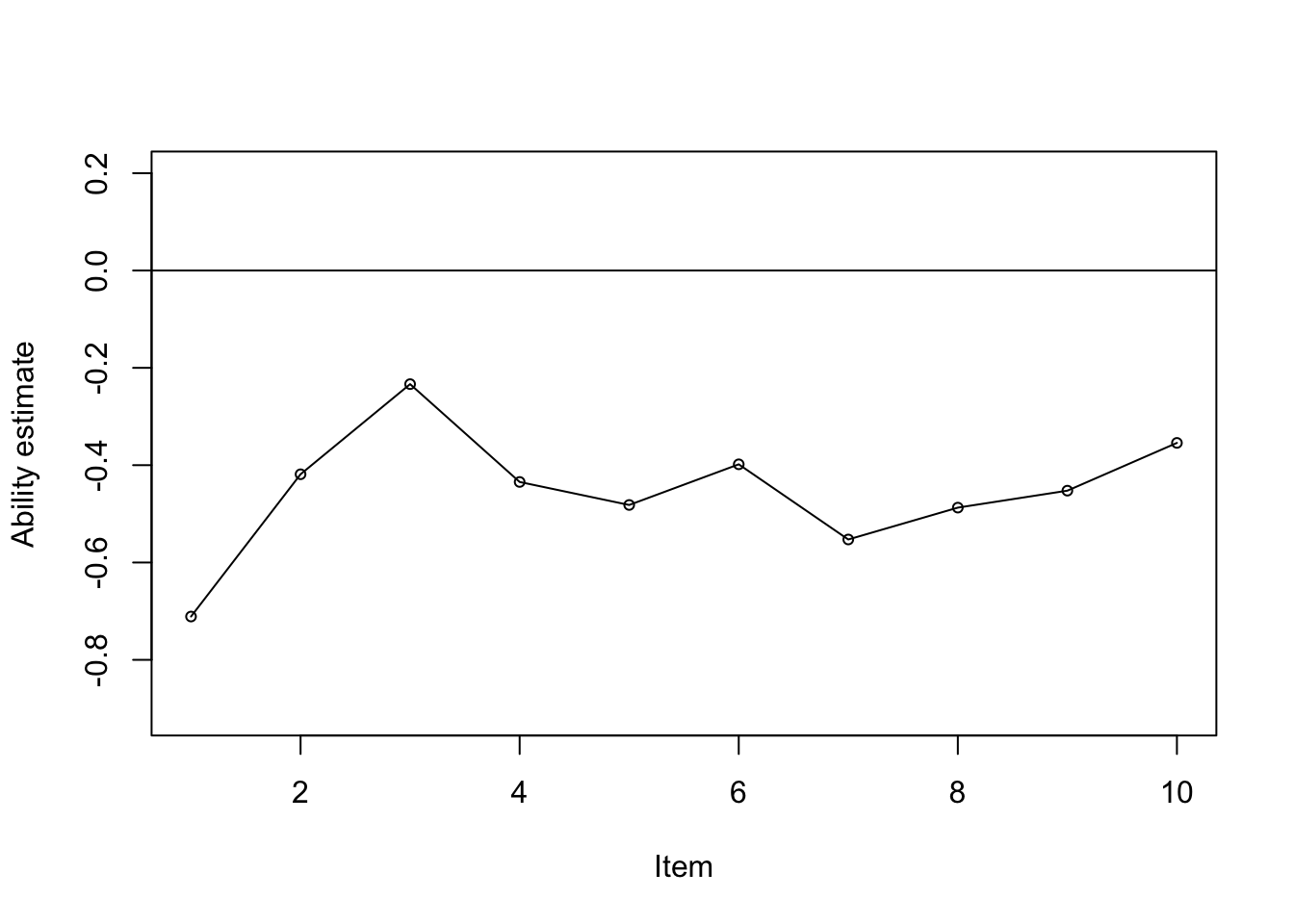
## Est. -0.711 -0.419 -0.233 -0.434 -0.482 -0.398 -0.553 -0.487 -0.452 -0.354
## SE 0.745 0.562 0.462 0.421 0.383 0.345 0.332 0.306 0.288 0.273
##
##
## Satisfied stopping rule:
## Length of test
##
## Final results:
## Length of adaptive test: 10 items
## Final ability estimator: Bayes modal (MAP) estimator
## Final prior distribution: N(0,1) prior
## Final standard error: asymptotic SE (ASE)
## Type of ASE formula: classic formula
## Final ability estimate (ASE): -0.349 (0.267)
## 95% confidence interval: [-0.872,0.174]
##
## Output was not captured!require(catR)Let’s have a look at the output and discuss a little about what we see.
The output first tells you which model you have used simulating the CAT. In our case, it is the Partial Credit Model (PCM).
Then it talks a little bit about the starting parameters. Here we can see that the item with the maximum information at the ability = 0 was used for the first item. We did not control for content balancing. You have to explicitly state that you want to control for content balancing.
Next the output talks about the adaptive parameters. The MFI was employed for item selection and the EAP was used for the ability estimate. Note that more often than not, the Bayes Modal, which is frequently described as the MAP, often have very similar results with the EAP.
The Stopping rule section tells us that the criterion is based on the length of items, which in this case we have fixed it to a maximum of 10.
The Randomesque method is used when you want to select a range of items that is considered as the next items that is best suited for the estimated ability. Within the range of items, say 5, the algorithm will randomly draw out 1. This often used to spread out the exposure and maintain item security. In our case, we did not enforce this method, so the algorithm will always select the next most optimal item for the estimated ability.
Now we have reached the Adaptive test details. This gives us the information of which 10 items were selected for the simulation. Nr is the index of the item. Item is the question that was given out. For example, item 21 is given in the first instance. The theta estimate (Est.) and the standard error (SE) is also provided for each item. That is the beauty of modern psychometric approaches. Everything is investigated at a item level rather than a scale. level.
Finally, what we have is the final result of the ability estimate.
Plot Simulation
## The plot was not captured!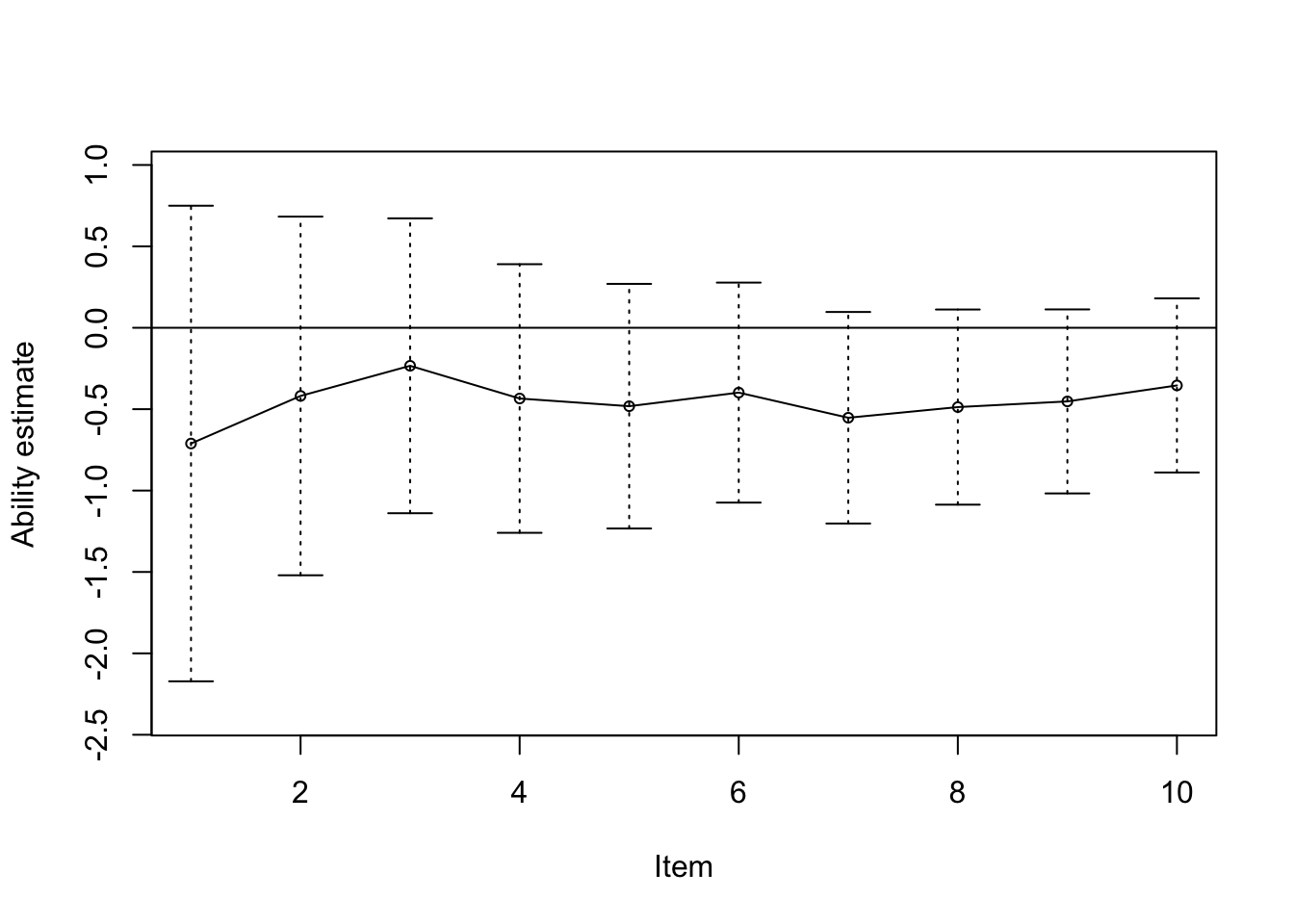
## The plot was not captured!Now we come to plotting and interpreting the plots!